Question 1031262: Find the equations of the bisectors of the interior angles of the triangle whose vertices are (0,4), (-4,-4) and (6,1).
Find the equation of the line that bisects the acute angle formed by the following lines.
a.) x-y=0 and x=0
b.) 7x-y=5 and y=x+1
Answer by robertb(5830)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let the points be P(0,4), Q(-4,-4) and R(6,1).
Then line PQ will have slope  , and the equation would be 2x - y + 4 = 0. , and the equation would be 2x - y + 4 = 0.
The line QR will have slope  , and the equation would be x - 2y - 4 = 0. , and the equation would be x - 2y - 4 = 0.
Then line PR will have slope  , and the equation would be x + 2y -8 = 0. , and the equation would be x + 2y -8 = 0.
For the angle bisector at angle Q, let (x,y) be any point on it. Then the distance of (x,y) from line PQ is 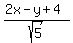 , while its distance from the line QR is , while its distance from the line QR is 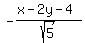 . (The negative sign denotes the fact that points (x,y) above the line x - 2y - 4 = 0 will give a net sign of negative for the expression x-2y-4 upon substitution.) . (The negative sign denotes the fact that points (x,y) above the line x - 2y - 4 = 0 will give a net sign of negative for the expression x-2y-4 upon substitution.)
==> 
==> 2x-y+4 = -x+2y+4 ==> 3x = 3y, or  . .
For the angle bisector at angle P, let (x,y) be any point on it. Then the distance of (x,y) from line PQ is 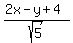 , while its distance from the line PR is , while its distance from the line PR is 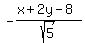 . (The negative sign denotes the fact that points (x,y) below the line x + 2y - 8 = 0 will give a net sign of negative for the expression x+2y-8 upon substitution.) . (The negative sign denotes the fact that points (x,y) below the line x + 2y - 8 = 0 will give a net sign of negative for the expression x+2y-8 upon substitution.)
==> 
==> 2x -y +4 = -x-2y+8 ==>  . .
By a similar procedure, it easily found that the angle bisector for angle R is simply  . .
a.) x-y=0 and x=0.
Let (x,y) be in the angle bisector with vertex at (0,0).
The distance of (x,y) from the line x=0 (the y-axis) is x, while the distance of (x,y) from the line x - y=0 is  . The negative sign is for the fact that upon substitution of the coordinates of (x,y) into x - y, the sign of the expression is negative. . The negative sign is for the fact that upon substitution of the coordinates of (x,y) into x - y, the sign of the expression is negative.
==>  , or , or  , after simplification. , after simplification.
b.) I leave up to you.
|
|
|