.
Given that cos t = 8/9 and that P(t) is a point in the fourth quadrant, find sin t.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Since cos(t) =  , you have
, you have
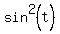 =
= 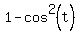 =
=  =
= 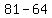 =
= 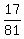 .
Hence, sin(t) = +/-
.
Hence, sin(t) = +/- 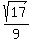 .
Now, what sign, "+" or "-", to choose?
Since P(T) is in QIV, what sign for sin(t) will you choose?
.
Now, what sign, "+" or "-", to choose?
Since P(T) is in QIV, what sign for sin(t) will you choose?
Comment from student: Thanks so much for the help! By the way, I'm thinking that the sign would be negative?
My response: you are right! Hope next time you will be able to solve similar problems on your own. Good luck!!!