SOLUTION: Write the given expression in terms of x and y only. sin(tan^−1(x) − tan^−1(y)) Find the exact value of the expression. tan(sin^−1(2/3)−cos^&

.


When solving problems like this, half of the success is to reformulate it reasonably.


So I will do it now.  We need to calculate  ,  where   = 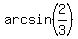  and   = .

So we have the angle    in Q1  with  = ,  and the angle    in Q1  with  = .

Since  = 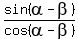, the plan is to calculate  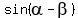and 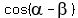.  //Making a good plan is the second half of the success. 

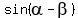To calculate    and 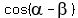 ,  we will use well known formulas of Trigonometry


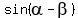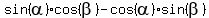 =   and 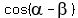  = 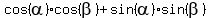.    (1)


   (Regarding these formulas, see the lesson  Addition and subtraction formulas  in this site). 


Looking into the formulas (1), you see that we need to know/to have the values    and    
in addition to the given values of    and  .  It is easy.  

First,  =  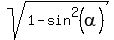=  =  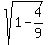= 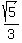. Second,  =  =  =  =  = .

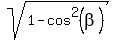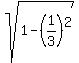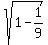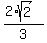Notice that the signs at square roots are chosen "+" since the angles  and  both lie in Q1.

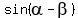Now you have everything to calculate  and 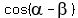 according to (1).  //Implementing the plan accurately is the third half of the success.


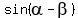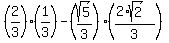 =  =  = .   (by the way, it shows that  lies in Q4).

 =  = . 

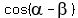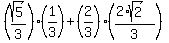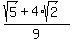And finally 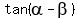  = 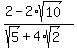.    (2)

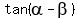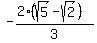If you rationalize the denominator in (2),  you will get the answer   = .

Answer. 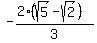 .