.
Please Find the general solution of:
sin(3x) - sin(x)= cos(2x)
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Apply the formula 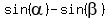 =
= 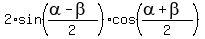 to the left side.
(Regarding this formula, see the lesson Addition and subtraction of trigonometric functions in this site).
You will get an equivalent equation
to the left side.
(Regarding this formula, see the lesson Addition and subtraction of trigonometric functions in this site).
You will get an equivalent equation
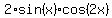 =
= 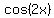 .
Simplify it further:
.
Simplify it further:
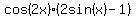 =
=  .
Then you have two equations:
(1) cos(2x) = 0 ---> 2x =
.
Then you have two equations:
(1) cos(2x) = 0 ---> 2x = 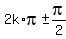 ---> x =
---> x = 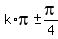 , k = 0, +/-1, +/-2, . . . ,
and
(2) 2*sin(x) = 1 ---> sin(x) =
, k = 0, +/-1, +/-2, . . . ,
and
(2) 2*sin(x) = 1 ---> sin(x) =  ---> x =
---> x =  and x =
and x =  , k = 0, +/-1, +/-2, . . . .
The union of the sets (1) and (2) is your solution.
, k = 0, +/-1, +/-2, . . . .
The union of the sets (1) and (2) is your solution.