Question 1031097: $3250 is invested at 5.5% compounded continuously. How long will it take for the balance to reach $6500? Please round your answer to two decimal places, if necessary.
Found 2 solutions by Cromlix, MathTherapy:
Answer by Cromlix(4381)   (Show Source):
You can put this solution on YOUR website! Hi there,
I assume the sum is annually
compounded.
100% + 5.5% = 105.5%
105.5% = 105.5/100 = 1.055 (factor)
3250 x 1.055^x = 6500
1.055^x = 6500/3250
1.055^x = 2
x log(1.055) = log(3250)
x = log(3250)/log(1.055)
x = 46.56 years
Hope this helps :-)
Answer by MathTherapy(10552)  (Show Source):
You can put this solution on YOUR website!
$3250 is invested at 5.5% compounded continuously. How long will it take for the balance to reach $6500? Please round your answer to two decimal places, if necessary.
Use the continuous compounding formula:  , and solve for t, the time, to get: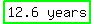 
Note that the INVESTMENT amounts ($3,250 and $6,500) DO NOT MATTER, since this is basically asking how long the investment takes to DOUBLE,
based on continuous compounding, at a 5.5% interest rate.
|
|
|
