Question 1030772: Hi. this lesson is really confusing me and I need help with it. These questions are confusing me. Please help me solve these problems.
For questions 3-5, find the first 4 terms and the 8th term of the recursively-defined sequence.
3. b1 = 2 and bk+1 = 3bk, for k>0
4. v1 = 0.75 and vn = (-2)vk-1 for n>1
5. c1 = 2, c2 = -1, and ck+2 = ck + ck+1 for k>0
6. Identify the sequence {-2, 2, -2, 2 ...} as arithmetic or geometric. Then find the common difference or ratio as appropriate.
7. Identify the sequence {-5, -2, 1, 4 ...} as arithmetic or geometric. Then find the common difference or ratio as appropriate.
8. The third and sixth terms of a geometric sequence are -75 and -9375 respectively. Find the first term, the common ratio, and an explicit rule for the nth term.
Answer by ikleyn(52787)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Hi. this lesson is really confusing me and I need help with it. These questions are confusing me. Please help me solve these problems.
For questions 3-5, find the first 4 terms and the 8th term of the recursively-defined sequence.
3. b1 = 2 and bk+1 = 3bk, for k>0
 = 2; = 2;  = = 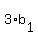 = 3*2 = 6, . . .
It is a geometric progression, first term 2, common ratio 3.
4. v1 = 0.75 and vn = (-2)vk-1 for k>1
It is a geometric progression, first term 0.75, common ratio -2.
5. c1 = 2, c2 = -1, and ck+2 = ck + ck+1 for k>0
6. Identify the sequence {-2, 2, -2, 2 ...} as arithmetic or geometric. Then find the common difference or ratio as appropriate.
It is a GP with the common ratio (-1).
7. Identify the sequence {-5, -2, 1, 4 ...} as arithmetic or geometric. Then find the common difference or ratio as appropriate.
It is an AP with the common difference 3.
8. The third and sixth terms of a geometric sequence are -75 and -9375 respectively.
Find the first term, the common ratio, and an explicit rule for the nth term. = 3*2 = 6, . . .
It is a geometric progression, first term 2, common ratio 3.
4. v1 = 0.75 and vn = (-2)vk-1 for k>1
It is a geometric progression, first term 0.75, common ratio -2.
5. c1 = 2, c2 = -1, and ck+2 = ck + ck+1 for k>0
6. Identify the sequence {-2, 2, -2, 2 ...} as arithmetic or geometric. Then find the common difference or ratio as appropriate.
It is a GP with the common ratio (-1).
7. Identify the sequence {-5, -2, 1, 4 ...} as arithmetic or geometric. Then find the common difference or ratio as appropriate.
It is an AP with the common difference 3.
8. The third and sixth terms of a geometric sequence are -75 and -9375 respectively.
Find the first term, the common ratio, and an explicit rule for the nth term.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
It looks like you know nothing about arithmetic and geometric progressions.
Read the lessons
- Arithmetic progressions
- Geometric progressions
in this site.
|
|
|