Question 1030513: The sum of three integers is
397. The sum of the first and second integers exceeds the third by
35. The third integer is
5 less than the first. Find the three integers.
Found 2 solutions by ankor@dixie-net.com, MathTherapy:
Answer by ankor@dixie-net.com(22740)   (Show Source):
You can put this solution on YOUR website! The sum of three integers is 397.
a + b + c = 397
The sum of the first and second integers exceeds the third by 35.
a + b = c + 35
The third integer is 5 less than the first.
c = a - 5
:
Replace c with (a-5) in the 1st and the 2nd equation
a + b + (a-5) = 397
2a + b = 397 + 5
2a + b = 402
and
a + b = (a-5) + 35
a - a + b = 35 -5
b = 30
:
In the equation 2a +b = 402, replace b with 30
2a + 30 = 402
2a = 372
a = 372/2
a = 186
then
c = 186 - 5
c = 181
:
Check this in the first equation
186 + 30 + 181 = 397
:
Find the three integers. 186, 30, 181
Answer by MathTherapy(10552)  (Show Source):
You can put this solution on YOUR website!
The sum of three integers is
397. The sum of the first and second integers exceeds the third by
35. The third integer is
5 less than the first. Find the three integers.
Let the first, second, and 3rd numbers, be x, y, and z
Then: x + y + z = 397 -------- eq (i)
Also, x + y = z + 35 ______x + y - z = 35 -------- eq (ii)
And, z = x - 5 -------- eq (iii)
2z = 362 -------- Subtracting eq (ii) from eq (i)
z, or 3rd numbe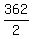r =  , or 
181 = x - 5 ------- Substituting 181 for z in eq (iii)
181 + 5 = x
x, or 1st number = 
186 + y + 181 = 397 -------- Substituting 186 for x, and 181 for z in eq (i)
367 + y = 397
y = 397 - 367, or 
|
|
|
