SOLUTION: A goldsmith has two gold alloys. The first alloy is 20% gold and the second alloy is 60% gold. How many grams of each alloy should be mixed to produce 80 grams that is 52% gold?

Take F grams of the 20% gold alloy and S grams of the 60% gold alloy.
Make sure that 

   F +    S = 80,         (1)   and
0.2F + 0.6S = 0.52*80.    (2) 

Solve this system for F and S:

   F +    S = 80,         (1)   and
0.2F + 0.6S = 41.6.       (2)       ( 41.6 = 0.52*80 )

You can solve the system using the substitution method.
Express S = 80 - F  from equation (1) and substitute it into equation (2). You will get

0.2F + 0.6*(80-F) = 41.6,
0.2F + 48 - 0.6F = 41.6,
-0.4F = 41.6 - 48,
-0.4F = -6.4,

F = 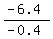 = 16.

So, the goldsmith should take 16 grams of the 20% gold alloy and 80-16 = 64 grams of the 60% gold alloy.

Check.  0.2*16 + 0.6*64 = 41.6 = 0.52*80.