Question 1030298: The path of a satellite orbiting the earth causes the satellite to pass directly over two tracking stations A and B, which are 85 mi apart. When the satellite is on one side of the two stations, the angles of elevation at A and B are measured to be 87.0° and 84.2°, respectively. (Round your answers to the nearest mile.)
(a) How far is the satellite from station A?
Answer: mi
(b) How high is the satellite above the ground?
Answer: mi
IMAGE BELOW
http://www.webassign.net/sprecalc7/6-5-031.png
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! The path of a satellite orbiting the earth causes the satellite to pass directly over two tracking stations A and B, which are 85 mi apart.
When the satellite is on one side of the two stations, the angles of elevation at A and B are measured to be 87.0° and 84.2°, respectively.
(Round your answers to the nearest mile.)
:
(a) How far is the satellite from station A?
A triangle ABC, is formed by the two stations and the satellite (C)
The three interior angles:
A: 180-87 = 93 degrees
B: 84.2 degrees
C: 180-84.2-93 = 2.8 degrees
Use the law of sines, the distance AC to the satellite is opposite B, 84.2 degrees
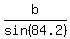 = = 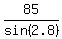
Cross multiply
.0488b = 85 * sin(84.2)
.0488b = 84.565
b = 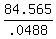
b = 1731 miles from Stn A to the Satellite
:
(b) How high is the satellite above the ground?
A point (P) on the earth directly below the satellite, forms a right triangle
with Station A: PCA,
the distance CP is opposite angle A, 87 degrees, hypotenuse = 1731 mi
Sin(87) = 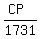
CP = 1731 * Sin(87)
CP = 1729 mi above the earth
|
|
|