SOLUTION: What is the number of solutions of the eqn : sin^8x + cos^6x = 1?

Algebra ->  Trigonometry-basics -> SOLUTION: What is the number of solutions of the eqn : sin^8x + cos^6x = 1?      Log On


   

Question 1030290: What is the number of solutions of the eqn : sin^8x + cos^6x = 1?
Answer by Edwin McCravy(20059) About Me  (Show Source):
You can put this solution on YOUR website!

There are infinitely many solutions:

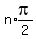n%2Aexpr%28pi%2F2%29 where n is any integer positive negative or 0. 

sin%5E8%28x%29%2Bcos%5E6%28x%29=1

%28sin%5E2%28x%29%29%5E4%2B%28cos%5E2%28x%29%29%5E3=1

%28sin%5E2%28x%29%29%5E4%2B%281-sin%5E2%28x%29%29%5E3=1

Let u=sin%5E2%28x%29

u%5E4%2B%281-u%29%5E3=1

u%5E4%2B%281-u%29%281-u%29%281-u%29=1

u%5E4%2B%281-u%29%281-2u%2Bu%5E2%29=1

u%5E4%2B1-2u%2Bu%5E2-u%2B2u%5E2-u%5E3=1

u%5E4-u%5E3%2Bu%5E2%2B2u%5E2-2u-u%2B1=1

u%5E4-u%5E3-u%5E2%2Bu=0

u%28u%5E3-u%5E2-u%2B1%29=0

It's easy to see that 1 is a solution
to the cubic polynomial in parentheses.
We use synthetic division

1|1 -1 -1  1
 |   1  0 -1
  1  0 -1  0

So we have factored to above as

u%28u-1%29%28u%5E2-1%29=0

And we can factor once more as

u%28u-1%29%28u-1%29%28u%2B1%29=0

That has solutions

u=0, u=1, u=-1

Since u=sin%5E2%28x%29

sin%5E2%28x%29=0, sin%5E2%28x%29=1, cross%28sin%5E2%28x%29=-1%29

We eliminate the third case because it will not give 
a real solution.

sin%28x%29=0, sin%28x%29=%22%22+%2B-+1

The first gives any multiple of p or np,
where n is any integer, positive negative or zero.

The second gives ±p/2 plus any multiple of 2p,

or p/2 + 2kp = (1+2k)p/2.
where k is any integer, positive negative or zero. 

That's all odd multiples of p/2  

Since all multiples of p are also multiples
of ±p/2, all solutions are the multiples of
p/2 

np/2                       <--- answer
(where n is any integer, positive negative or zero.)

So the number of solutions is INFINITY!

Edwin