SOLUTION: find the largest value of the fraction A-B/A+B where A and B lies between 1 to 50

Algebra ->  Finance -> SOLUTION: find the largest value of the fraction A-B/A+B where A and B lies between 1 to 50      Log On


   

Question 1029995: find the largest value of the fraction A-B/A+B where A and B lies between 1 to 50
Found 2 solutions by Fombitz, Edwin McCravy:
Answer by Fombitz(32388) About Me  (Show Source):
You can put this solution on YOUR website!
You want the maximum difference in the numerator which also gives you the minimum denominator.
f=%2850-1%29%2F%2850%2B1%29=49%2F51

Answer by Edwin McCravy(20063) About Me  (Show Source):
You can put this solution on YOUR website!
When it is necessary to type algebra all on one line,
then you MUST have parentheses around the numerator and
denominator to show where the numerator and denominator
begin and end.

So you should have typed (A-B)/(A+B) not A-B/A+B

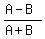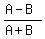In other words, you want %28A-B%29%2F%28A%2BB%29, not A-B%2FA%2BB,
for without parentheses, A-B/A+B is taken to mean A-B%2FA%2BB

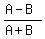The largest value of %28A-B%29%2F%28A%2BB%29 is when the numerator
is as large as possible and the denominator is as small as
possible. This is when A is 50 and B is 1.

So the largest value of %28A-B%29%2F%28A%2BB%29 is when A=50 and B=1, or
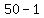
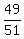50-1%29%2F%2850%2B1%29%22%22=%22%2249%2F51

---------------------------

However if the problem were the largest value of A-B/A+B, as you 
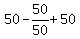typed it above, the largest value would be 50-50/50-50 = 50-50%2F50%2B50 = 50-1+50 = 99.

Parentheses are always necessary when algebra is typed all on one line.

Edwin