Question 1029948: A tabletop has the shape of a regular decagon with a radius of 9.5 inches. What is the area of the tabletop to the nearest square inch?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! decagon is ten sides polygon.
radius = 9.5 inches.
there is an online calculator that will calculate the area for you.
that calculator can be found here.
http://www.calculatorsoup.com/calculators/geometry-plane/polygon.php
the display of looking for the area of a decagon, given the radius is shown below.
look for further comments beneath that display.
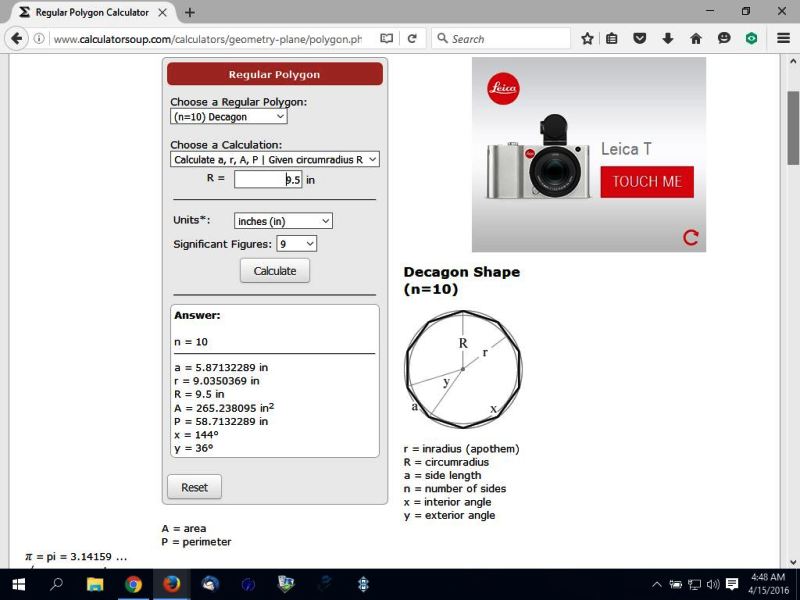
this calculator tells you that the area is equal to 265.238095 square inches.
if you did not have access to this calculator, and you did not know the formula shown, you could have figured it out as follows?
take 360 degrees and divide it by 10 and you get that the central angle of each of the triangle formed within the decagon is equal to 36 degrees.
fyi, this is also the external angle of the decagon.
fyi, the internal angle of the decagon is 180 - 36 = 144 degrees.
your immediate interest is the central angle of 36 degrees.
since the radius is 9.5 inches, you have 10 isosceles triangles formed, each with a vertex of 36 degrees and side lengths of 9.5 inches each.
you want to find the area of each of these triangles and then multiply that by 10 to get the area of the decaton.
drop a perpendicular from the vertex to the base.
it divides the isosceles triangle into two right triangles that are congruent to each other.
solve for the altitude and then for the base of one of these triangles as follows.
altitude = 9.5 * cos(18).
base = 9.5 * sin(18).
you are using basic trig formulas of:
cos(18) = adjacent / hypotenuse = adjacent / 9.5.
from this you solve for adjacent to get adjacent = 9.5 * cos(18).
sin(18) = opposite / hypotenuse = opposite / 9.5.
from this you solve for opposite3 to get opposite = 9.5 * sin(18).
adjacent is the altitude of the triangle.
opposite is the base.
you will find that the adjacent of one of these right triangle is equal to 9.035036905.
you will find that the opposite of one of these right triangles is equal to 2.935661447.
since the right triangle is one half of the isosceles triangle, you will then find that:
the altitude of the isosceles triangle is the same = 9.035036905.
the base of the isosceles triangle is 2 * the base of the right triangle = 5.871322893.
the area of the isosceles triangle is then equal to 1/2 * base * height which is equal to 1/2 * 9.035036905 * 5.871322893 which is equal to 26.52380951 square inches.
since there are 10 identical isosceles triangles in the decagon, then the area of the decagon is equal to 10 * 26.52380951 which is equal to 265.2380951 square inches.
you get the same area as the calculator gave you, indicating that you did this correctly.
round your answer to the nearest square inch and you have the area is equal to 265 square inches.
|
|
|