Question 1029807: An auditor for American Health Insurance reports that 20% of policyholders submit a claim during the year. 15 policyholders are selected randomly. What is the probability that at least 3 of them submitted a claim the previous year?
Answer by mathmate(429)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Question:
An auditor for American Health Insurance reports that 20% of policyholders submit a claim during the year. 15 policyholders are selected randomly. What is the probability that at least 3 of them submitted a claim the previous year?
Solution:
The probability of success (submitted a claim) is p=0.20, and remains constant throughout.
Size of sample, n=15, and policyholders are selected randomly (assumed independently as well).
x=3, number of successes for which probability is required.
The above data satisfies the necessary conditions for modelling with the binomial distribution, which estimates the probability of x successes out of n each with a probability of p as:
P(X=x,p,n)=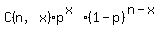
where
x=3
n=15
p=0.2 and
C(n,x)=n!/(x!(n-x)!) is the number of combinations for x objects chosen from n.
Hence
P(X=x,p,n)=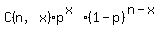
=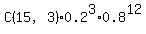
=455*0.008*0.0687195
=0.25014
For more explanations on the conditions required to model with binomial distributions, and more examples, see:
http://www.euclid.host-ed.me/probability/binomialDistribution.html
|
|
|