Question 1029791: Let x=k be a vertical assymptote of the graph of y=((x^2-2x-15)/(x^3-14x^2+23x+110)). Find the sum of all possible distinct values k.
Any help is greatly appreciated!!!
Thank you in advance!
P.S. The answer is 9
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39630)   (Show Source):
You can put this solution on YOUR website! Factorize the denominator according to Rational Roots Theorem.
Some of the roots to check for are -1, -2, -4, -5, and 1, 2, 4, 5; and there may be others, according to the theorem, but the smaller sized roots are probably what will be needed.
Going through synthetic division to check for -2 as a root, you will find 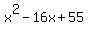 with remainder 0. This quadratic factor will have roots according to whatever method you want, of 5 and 11. The denominator of your equation's right hand member is therefore  .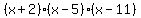
Now factorize your num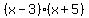erator.
 , your numerator.
Reexpress your equation as  .
Any factors common to numerator and denominator? No. The factors of the denominator form vertical asymptotes, and there are THREE of them. These three x values for the asymptotes are -2, 5, and 11.
These results do not agree with your reported answer sum of 9.
You can try to rework a solution and MAYBE find any mistake I made.
Answer by ikleyn(52879)  (Show Source):
You can put this solution on YOUR website! .
Let x=k be a vertical asymptote of the graph of y=((x^2-2x-15)/(x^3-14x^2+23x+110)). Find the sum of all possible distinct values k.
Any help is greatly appreciated!!!
Thank you in advance!
P.S. The answer is 9
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
There is much simpler solution.
1. It is easy to guess the roots of the numerator. They are 3 and -5.
2. No one of them is the root of the denominator.
Hence, the asymptotes x = k are all the roots of the denominator and only they.
3. But the sum of the roots of the denominator is equal to the coefficient at  of the denominator, taken with the opposite sign, i.e. 14.
By the way, this solution demonstrates that your answer "9" is wrong.
|
|
|
