.
√3*sin(x/2)+cos(x/2)=0
(π≤x<4π)
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
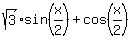 =
=  ---> (divide bith sides by 2) --->
---> (divide bith sides by 2) --->
 =
=  . (1)
Notice that
. (1)
Notice that  =
= 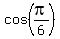 and
and  =
=  .
Therefore, you can rewrite (1) as
.
Therefore, you can rewrite (1) as
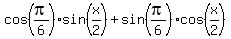 =
=  . (2)
Now apply the addition formula for sine
. (2)
Now apply the addition formula for sine 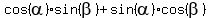 =
= 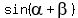 .
You will get instead of (2)
.
You will get instead of (2)
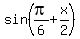 =
=  .
Then pi/6 + x/2 =
.
Then pi/6 + x/2 =  , k = 0, +/-1, +/-2, . . .
Hence x =
, k = 0, +/-1, +/-2, . . .
Hence x = 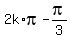 .
To get the given interval for x, take k = 1 and k = 2.
You will have two solutions x =
.
To get the given interval for x, take k = 1 and k = 2.
You will have two solutions x = 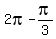 =
=  and x =
and x = 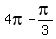 =
= 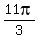 .
Answer. There are two solutions in the given interval.
They are x =
.
Answer. There are two solutions in the given interval.
They are x =  and x =
and x = 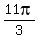 .
.