Question 1029162: A shipment of 100 tape recorders contain 30 that are defective. if 10 of them are randomly chosen for inspection.what z d probability that 2 of the 10 will be defective
Answer by mathmate(429)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Question:
A shipment of 100 tape recorders contains 30 that are defective. if 10 of them are randomly chosen for inspection.what is the probability that 2 of the 10 will be defective?
Solution:
This problem could be mistaken to be a binomial distribution by taking the defective rate to be constant at 30%. However, careful scrutiny reveals that the 30 defectives out of 100 does not remain constant as we withdraw samples from the lot, which invalidates application of the binomial distribution, or at least renders it an approximation.
The hypergeometric distribution comes to our rescue in this situation, as follows:
A=number of defectives
B=number of non-defectives
a=number of defectives sampled
b=number of non-defectives sampled
then
P(a,b,A,B)=C(A,a)C(B,b)/C(A+B,a+b)
where
C(n,x)=n!/(x!(n-x)!) the binomial coefficient.
Here
A=number of defectives=30
B=number of non-defectives=70
a=number of defectives sampled=2
b=number of non-defectives sampled=8
P(a,b,A,B)
=P(2,8,30,70)
=C(70,8)C(30,2)/C(100,10)
=9440350920*435/17310309456440
=4459185/18796757
=0.23723 (to 5 figures)
An approximation using the binomial distribution gives
P(2,10,0.3)
=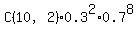
=45*0.09*0.05764800999999996
=0.23347
which is close, but not the same as the previous result.
|
|
|