SOLUTION: A boat takes 3 hours to go 12 miles upstream. It can go 18 miles downstream in the same time. Find the rate of the current and the rate of the boat in still water.​ (Hint: Be

The boat speed moving upst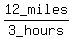ream is  =  = 4 mph. 

It is the boat speed relative to the river banks, when the boat moves upstream.
As they explained in the "Hint" section, this speed is the difference of the boat speed in still water u 
and the current speed v. So, your first equation is 

u - v = 4.    (1)

The boat speed moving downstream is 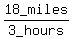 =  = 6 mph. 

Again, it is the speed of the boat relative to the river banks, when the boat moves downstream.
As they explained in the "Hint" section, this speed is the sum of the boat speed in the still water u 
and the current speed v. So, your second equation is 

u + v = 4.    (2)

Now, you should solve this system of the two equations

u - v = 4.    (1)
u + v = 6.    (2)

Add them to get 2u = 4 + 6 = 10,  u =  = 5.
Thus the speed of the boot in still water is 5 mph.

Then from (2) you have v = 6 - u = 6 - 5 = 1 mph.

Answer.  The rate of the current is 1 mile per hour.  The rate of the boat in still water is 5 miles per hour.