Question 1028785: can someone help answer these twin questions?? they don't make any sense, thanks
#1 Factor the expression on the left side of the equation. Then solve the equation.
x3 − 2x2 − 5x = 0
A. 0, -1 +/- sqrt 24
B. -5, 0, 3
C. 0, 1 +/- sqrt 6
D. 0, -1 +/- sqrt 6
#2 Factor the expression on the left side of the equation. Then solve the equation.
x6 + 128x3 + 4096 = 0
A. 4, 2 +/- 2i*sqrt 3
B. 4 multiplicity of 2, 2 +/- 2i*sqrt3 multiplicity of 2
C. -4, 2 +/- 2i*sqrt 3
D. - 4 multiplicity of 2, 2 +/- 2i*sqrt3 multiplicity of 2
Answer by ikleyn(52776)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
#1 Factor the expression on the left side of the equation. Then solve the equation.
x^3 - 2x^2 - 5x = 0
A. 0, -1 +/- sqrt 24
B. -5, 0, 3
C. 0, 1 +/- sqrt 6
D. 0, -1 +/- sqrt 6
~~~~~~~~~~~~~~~~~~~~~
Factor:
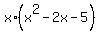 = =  .
Solve the equation .
Solve the equation 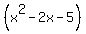 = =  . Apply the quadratic formula . Apply the quadratic formula
 = =  = = 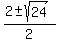 = = 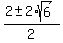 = = 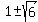 .
The roots of the original equation are 0, .
The roots of the original equation are 0, 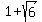 and and 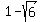 .
The answer is option C. .
The answer is option C.
#2 Factor the expression on the left side of the equation. Then solve the equation.
x6 + 128x3 + 4096 = 0
A. 4, 2 +/- 2i*sqrt 3
B. 4 multiplicity of 2, 2 +/- 2i*sqrt3 multiplicity of 2
C. -4, 2 +/- 2i*sqrt 3
D. - 4 multiplicity of 2, 2 +/- 2i*sqrt3 multiplicity of 2
Factor
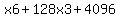 = = 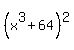 . (1)
Now solve . (1)
Now solve
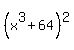 = =  . (2)
It is reduced to . (2)
It is reduced to
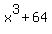 = =  , (3) , (3)
 = = 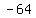 , ,
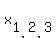 = =  , , 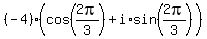 , , 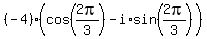 , or, which is the same , or, which is the same
 , , 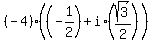 , , 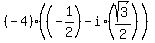 , or, which is the same again , or, which is the same again
 , , 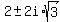 . (4).
Thus the solution of (3) are the roots (4).
Hence, the solution of (1) are the roots listed under the option D) . (4).
Thus the solution of (3) are the roots (4).
Hence, the solution of (1) are the roots listed under the option D)
|
|
|