|
Question 1028733: A ball is thrown upward with an initial velocity of 50 feet per second. The height h (in feet) of the ball after t seconds is given by h=-16^2+50t. At the same time, a balloon is rising at a constant rate of 20 feet per second. Its height h in feet after seconds is given by h=20t.
a.) when do the ball and the balloon reach the same height?
b.) when does the ball reach its maximum height?
c.) when does the ball hit the ground?
Please help me, gladly appreciated <3
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! There are to functions of time, and time is measured from the same moment taken at  fro both functions. (That is not very clearly stated in the problem, but your teacher thinks it is understood to be that way). fro both functions. (That is not very clearly stated in the problem, but your teacher thinks it is understood to be that way).
The function  is a very realistic representation of what the height (in feet) of a ball would be is a very realistic representation of what the height (in feet) of a ball would be  seconds after it is kicked up (or shot up) from the ground. (A physics teacher would like that equation). seconds after it is kicked up (or shot up) from the ground. (A physics teacher would like that equation).
The function  must represent the height (in feet) of a balloon must represent the height (in feet) of a balloon  seconds after the ball is kicked/shot up. (I believe this is not very realistic for all seconds after the ball is kicked/shot up. (I believe this is not very realistic for all  , and it would take some skill on the part of the balloon pilot to achieve that for some time). , and it would take some skill on the part of the balloon pilot to achieve that for some time).
a.) The ball and the balloon reach the same height when




Obviously, that would be true for
 ---> --->
So, the ball and the balloon reach the same height "after  ". ".
That means 1.875 seconds after  , which should be the time the ball was kicked up (or shot up). , which should be the time the ball was kicked up (or shot up).
b.) The function  is a quadratic function that has a maximum for a certain value of is a quadratic function that has a maximum for a certain value of  , and that value represents when the ball reaches its maximum height. , and that value represents when the ball reaches its maximum height.
If you want to use a formula given in class, there is no need to think, you just apply the memorized formula.
Just in case, the formula said the the maximum for a function  with with  happens when happens when
 . .
Of course, with  , ,
you have  instead of instead of  and and  instead of instead of  , ,
but it is the same kind of unction, with  , ,  and and  . .
So, the maximum occurs when 
The ball reaches maximum height after  . .
Hey, the means that when the ball meets the balloon (at t=1.875 seconds), the ball is already on its way down.
If you do not like to memorize stuff just because someone said so,
 --> --> --> --> --> --> --> --> . .
For 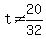 , , 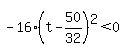 and and  . .
For  , ,  and and  has its maximum value. has its maximum value.
c.) The ball is at groune level when  . .
 --> --> --> -->
So  for for 
So the ball leaves the ground at  and hits the ground after and hits the ground after  . .
Here is a graph:

NOTE:
Math is use every day (by a few people) to do the calculations they need to do in real life. Some people think they do not need math.
Thirty-five years ago most people thought they did not need a microwave oven, because they did not know about them and they did not know how to use them. I spent a lot of money on one and enjoyed efficient cooking for the next 21 years. (Then it broke down and I got a new one). By then, most of those who said a microwave oven was not necessary had changed their mind. Would that ever happen with people who think you do not need math?
|
|
|
| |