|
Question 102873: PLEASE HELP TONIGHT if possible! This problem doesn't come from a textbook, but it is the only one on the worksheet that I cannot solve. Here it goes:
The graph of the square function (f(x) = x^2) has been transformed by rotating the graph about the x-axis, pushing the entire graph down 5 units, and then left 8 units.
Write the equation of the transformed graph.
Thanks so much! If you can get it to me tonight, that would be great, since it is due by midnight!!!
Found 3 solutions by rapaljer, bucky, edjones:
Answer by rapaljer(4671)   (Show Source): (Show Source):
You can put this solution on YOUR website! Rotating the graph y=x^2 about the x-axis does not change it. Dropping the graph down 5 units is like subtracting the value of 5 from the x^2, and shifting the graph left 8 units is like adding 8 to the x. The equation is  , and the graph should look like this: , and the graph should look like this:
R^2 Retired = R^3 from SCC
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! You start with:
.
f(x) = x^2
.
You can rotate it about the x-axis by changing the sign of the function. Call the new function
g(x). So for the first translation (about the x-axis), we have:
.
g(x) = -x^2
.
Next you want to shift the graph down by 5 units. Do this by just subtracting 5 from the
function. So now we have two translations and the function is:
.
g(x) = -x^2 - 5
.
We have one more translation to do. To shift the graph to the left 8 units, replace x
by x + 8. [Yep. The +8 shifts the graph to the left. If you had used -8, the graph would
shift to the right.] Anyhow, the resulting change to g(x) is:
.
g(x) = -(x + 8)^2 - 5
.
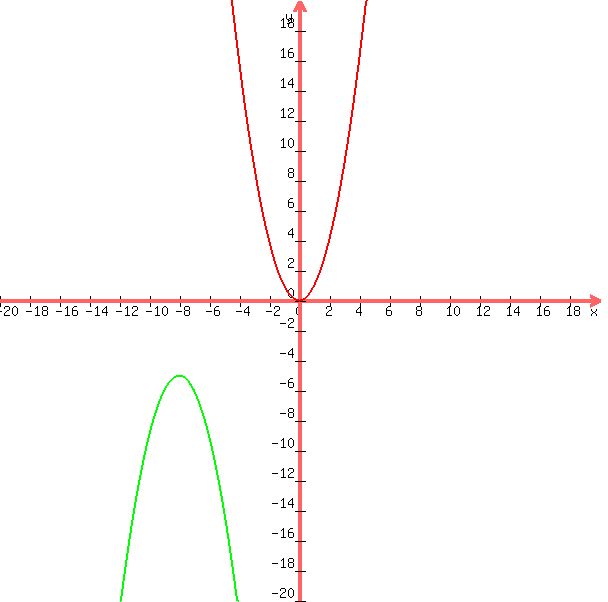
That's the answer. You might want to try plotting a few points of both functions just to
satisfy yourself of the shifts. Here's a graph of the two. The red graph is f(x) and the
green graph is g(x).
.
.
Hope this helps you out and that you can understand how the answer comes about.
.
Answer by edjones(8007)   (Show Source): (Show Source):
You can put this solution on YOUR website! -(x-8)^2-5
The 1st minus causes the parabola to be rotated about the x axis. The -8 moves it 8 units rightward and the -5 moves it 5 units downward.
Ed

|
|
|
| |