Question 1028712: I am stuck on this. Any help will be appreciated. Thanks!
If log_a(x)=2, log_a(y)=4, and log_a(z)=6, what is the value of log_a((y^2)/((x^2)√(z))
The listed answers are -2, -1, 0, 1, 2, and 3. Now I know that 'a' is unknown. So I assume that I need to use one of the properties to get an answer like log_a1=0, log_aa=1, etc. Using these I was only able to get it to 3log_a(2/6). Any help will be appreciated.
Found 3 solutions by richard1234, MathTherapy, Natolino1983:
Answer by richard1234(7193)   (Show Source): (Show Source):
Answer by MathTherapy(10555)   (Show Source): (Show Source):
You can put this solution on YOUR website! I am stuck on this. Any help will be appreciated. Thanks!
If log_a(x)=2, log_a(y)=4, and log_a(z)=6, what is the value of log_a((y^2)/((x^2)√(z))
The listed answers are -2, -1, 0, 1, 2, and 3. Now I know that 'a' is unknown. So I assume that I need to use one of the properties to get an answer like log_a1=0, log_aa=1, etc. Using these I was only able to get it to 3log_a(2/6). Any help will be appreciated.

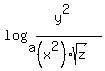
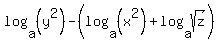

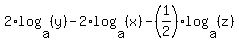
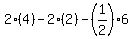 = 8 - 4 - 3 = = 8 - 4 - 3 = 
Answer by Natolino1983(23)   (Show Source): (Show Source):
You can put this solution on YOUR website! We will use this 3 properties 1)log_a (x×y) = log_a(x) + log_a (y)
2)log_a (x/y) = log_a (x) - log_a(y)
3)log_a(x^y) = y×log_a(x)
Therefore log_a ((y^2/(x^2×sqrt(z)) = log_a(y^2) - (log_a(x^2×sqrt(z)) (p.2)
= log_a(y^2) - (log_a(x^2) +log_a(sqrt(z)) (p.1)
=2×log_a(y) -(2×log_a(x) +log_a(z)/2) (p.3)
Replacing: 2×4 - (2×2 +6/2) =8 - 7 = 1
(Obs: sqrt(z) =z^(1/2) )
|
|
|