SOLUTION: If A is skew-symmetric matrix,show that the elements in the main diagonal are all zero.

Algebra ->  Matrices-and-determiminant -> SOLUTION: If A is skew-symmetric matrix,show that the elements in the main diagonal are all zero.      Log On


   

Question 1028695: If A is skew-symmetric matrix,show that the elements in the main diagonal are all zero.
Answer by robertb(5830) About Me  (Show Source):
You can put this solution on YOUR website!
If A is a nxn skew symmetric matrix, then -A+=+A%5Et.
Let A have main diagonal elements of 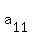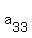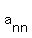a%5B11%5D, a%5B22%5D, a%5B33%5D, ...,a%5Bnn%5D.
If the transpose of A is obtained, then the position of the main diagonal elements are preserved, because they are the pivot elements. Since the transpose of A is supposed to be equal to -A, this means that the main diagonal elements 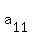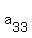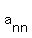-a%5B11%5D, -a%5B22%5D, -a%5B33%5D, ...,-a%5Bnn%5D of -A must be equal to a%5B11%5D, a%5B22%5D, a%5B33%5D, ...,a%5Bnn%5D.
==> a%5B11%5D+=+-a%5B11%5D ==> a%5B11%5D+=+0,
a%5B22%5D+=+-a%5B22%5D ==> a%5B22%5D+=+0,
a%5B33%5D+=+-a%5B33%5D ==> a%5B33%5D+=+0,...
a%5Bnn%5D+=+-a%5Bnn%5D ==> a%5Bnn%5D+=+0.
Therefore, the main diagonal elements of A are all 0.