SOLUTION: Solve the linear system by row-reducing the corresponding augmented matrix: -w+x-z=14 -w+x-y=-1 w-2x+y-z=4 -2w+x-y+4z=-19 b) Find the determinant of the coefficient matrix A

Write it this way:





R1<->R3



R1+R2<->R2

 

R1+R3<->R3



2R1+R4->R4



-1R2->R2



R2+R3->R3



3R2+R4->R4



-1R3->R3



2R3+R4->R4



Convert back to a system of equations:



or



Solve the bottom equation, get z=-35/6
Substitute in 3rd equation, get x=17/6
Substitute those in 2nd equation, get y=55/6
Substitute those in 1st equation, get w=-16/3

Coefficient matrix:



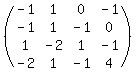Determinant of coefficient matrix:



R3+R2->R2



R4+R3->R3



We expand about the 3rd column,
which contains only -1 other than 0's

R4+R3->R3



We determine by the sign scheme whether
we are to use the -1 as it is as a multiplier
or whether we are to change its sign.  Here
is the "checkerboard" sign scheme:



We find that that element -1 is in a "-" position
in the checkerboard sign scheme, so we change the
sign of the -1 to +1 and multiply it by the 3x3
minor determinant gotten by omitting the row and 
column of the -1

So changing the sign of -1 to 1 and multiplying it
by the minor 3x3 determinant we have:




 
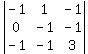-1*R1+R3->R3



We expand about the 1st column, which contains 
only -1 other than 0's

We determine by the sign scheme whether
we are to use the -1 as it is as a multiplier
or whether we are to change its sign.  Here
is the "checkerboard" sign scheme:
""-""


We find that that element -1 is in a "+" position
in the checkerboard sign scheme, so we leave the
sign of -1 and multiply it by the 2x2
minor determinant gotten by omitting the row and 
column of the -1

multiplying the -1 by the minor 3x3 determinant 
we have:

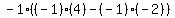
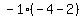
(-1(-6)}}}

I'll let you do the last one yourself. Here are
A-inverse and A-transpose:

  

Edwin