Question 1028452: A box has a base whose length is twice the width. The volume of the box is 70,000 cubic inches. A) find a function for the surface area of the box. B) What are the dimensions of the box that minimizes the surface area? Round your dimensions to the nearest hundredth. I've tried everything I cant seem to figure it out
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! here's what i got.
volume of the box = l*w*h
if you let v = volume, then you get v = l*w*h
l = length
w = width
h = height.
l*w = area of the base
l*h = = area of the side along the length.
w*h = area of the side along the width.
surface area of the box = 2*l*w + 2*l*h + 2*w*h
if you let s = surface area of the box, then you get s = 2*l*w + 2*l*h + 2*w*h
you are given that the length is equal to 2 * the width.
this means that l = 2*w
therefore you can replace l with 2*w.
v = l*w*h becomes v = 2*w*w*h which becomes v = 2*w^2*h
s = 2*l*w + 2*l*h + 2*w*h becomes s = 2*2*w*w + 2*2*w*h + 2*w*h which becomes s = 4*w^2 + 4*w*h + 2*w*h
so far you have:
v = 2*w^2*h
s = 4*w^2 + 4*w*h + 2*w*h
since the volume = 20,000, v = 2*w^2*h becomes 20,000 = 2*w^2*h
you can solve for h to get h = 20,000/(2*w^2) which can be simplified to h = 10,000/w^2
you now have:
v = 2*w^2*h
s = 4*w^2 + 4*w*h + 2*w*h
h = 10,000/w^2
in the surface area equation of s = 4*w^2 + 4*w*h + 2*w*h, you can replace h with 10,000/w^2 to get:
s = 4*w^2 + 4*w*10,000/w^2 +2*w*10,000/w^2
this equation can be simplified to:
s = 4*w^2 + 40,000/w + 20,000/w
simplify this to get s = 4*w^2 + 60,000/w, which can be rewritten as:
s = 4*w^2 + 60,000&w^-1
believe it or not, but this equation has a minimum.
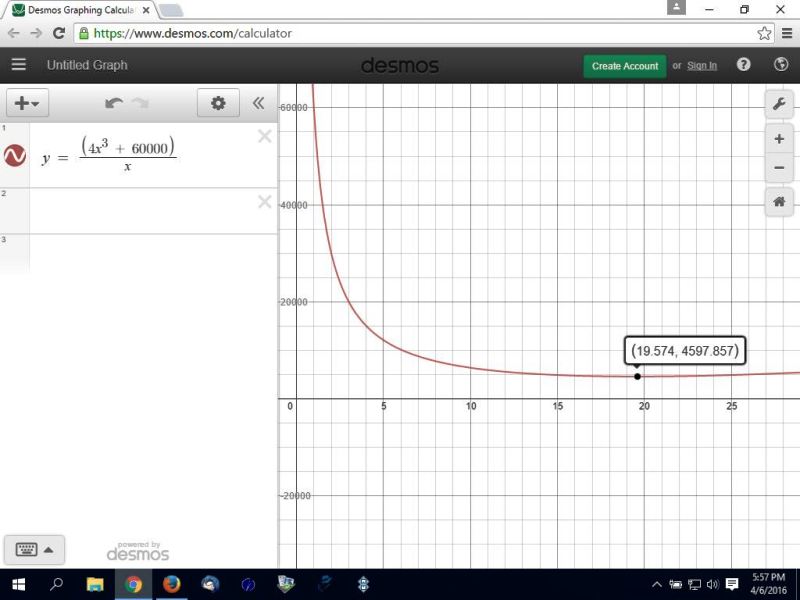
i graphed it and the graphing software told me that the minimum value of the curve is when w = 19.574
i then took the derivative of the equation to find the minimum point through the use of calculus.
the derivative of the equation is 8*w - 60,000/w^2
i set that equation equal to 0 to get 8*w - 60,000/w^2 = 0
i multiplied both sides of the equation by w^2 to get 8*w^3 - 60,000 = 0
i solve for w to get w = (60,000/8)^(1/3) = 19.57433821
the graph and the derivative equation agree, so i'm confident that's the solution.
now that you have w, it's an easy matter to figure out the values of the length and the height.
from the equation of h = 10,000/w^2, you get h = 26.09911761
from the equation of l = 2*w, you get l = 39.14867641
those are the values you are looking for.
l = 39.14867641
w = 19.57433821
h = 26.09911761
using these values, you get:
v = l*w*h = 20,000
s = 2*l*w + 2*l*h + 2*w*h = 4597.856594
this agrees with what the graph shows is the value of s.
you can also get the same value when you use the surface3 area equation of s = (4*w^3+60000)/w.
you can round the numbers as required.
i left them the way my calculator showed them to be.
here's the graph:
|
|
|