|
Question 1027848: Consider the functions
f(x) = sqrt((x+1)/(x-1)) and g(x) = sqrt(x+1)/sqrt(x-1)
Explain why f and g are not the same function.
Answer by Theo(13342)   (Show Source):
You can put this solution on YOUR website! f(x) = 
g(x) =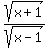 
they look like the same function to me.
we'll graph both functions to see if that's true or not.
here's the graph of f(x) =
here's the graph of g(x) =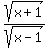
as you can see, they are not the same function.
they are the same function when x is positive.
here's a spreadsheet of the data for x = -5 to x +5.
to make a long story short, the basic difference is as follows:
with f(x) = , the numerator and divisor are within the same square root sign.
if the numerator is negative and the denominator is negative, then the result is positive.
the square root of a positive number is valid, so the square root is allowed and it can be graphed.
with g(x) = 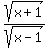, the numerator is under its own square root sign and the denominator is under its own square root sign.
if either the numerator is negative, or the denominator is negative, or botth are negative, then the result will be invalid because you can't take the square root of a negative number.
in general, square root of (a/b) is equal to square root of (a) / square root of (b).
this is true when both the numerator and denominator are positive.
when either the numerator or denominator or both are negative, then this is not true.
you then run into square root of a negative number, which is not valid.
if a is negative and b is positive, then:
sqrt(a/b) is not allowed because a/b is negative.
sqrt(a)/sqrt(b) is not allowed because a is negative.
likewise, if a is positive and b is negative, then:
sqrt(a/b) is not allowed because a/b is negative.
sqrt(a)/sqrt(b) is not allowed because b is negative.
if both a and b are negative, then:
sqrt(a/b) is allowed because a/b is positive.
sqrt(a)/sqrt(b) is not allowed because a is negative and because b is negative.
|
|
|
| |
