Question 1027829: Let S be the relation on N such that xSy means xy is a perfect square. Show that S is an equivalence relations. Write down all numbers no greater than 30 from one of its equiavalence classes
Answer by robertb(5830)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1. S is reflexive: It is obvious that xSx is true.
2. S is symmetric: xSy true implies that ySx is also true, because xy = ys is a perfect square.
3. S is symmetric.
xSy ==> xy =  for some integer k ==> for some integer k ==>  is an integer. is an integer.
ySz ==> yz = 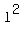 for some integer l ==> for some integer l ==>  is an integer. is an integer.
==> xz is an integer that is a perfect square, since, 
Therefore S is an equivalence relation.
E.g., [16] = {(16,1), (8,2), (4,4), (2,8), (1,16)}
|
|
|