|
Question 1027807: Please help me with these problem did any of this before.
Give an example of each of the following:
a. A function with vertical asymptotes at x=-3 and x=1, and a horizontal asymptote at y=2.
b. A word problem whose solution is 12!/9!3!
c. The equation of an ellipse with vertices at (0,0) and (-8,0).
d. A logarithmic expression equivalent to 5.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! a. To have those vertical asymptotes, a rational functions should have in the denominator the factors
 and and  . .
With  for a denominator for a denominator
a rational function with  for a horizontal asymptote for a horizontal asymptote
must have for a numerator a quadratic polynomial with  for a leading coefficient. for a leading coefficient.
 is a suitable numerator for that, and its value for is a suitable numerator for that, and its value for  and for and for  is not zero. is not zero.
So,  has all the required asymptotes. has all the required asymptotes.
FURTHER EXPLANATION:
A rational function may have vertical asymptotes at the values of  that make that make
the denominator zero.
So,  does not exist for does not exist for  , ,
and has  as a vertical asymptote, as a vertical asymptote,
because at valued close to  the numerator is close to the numerator is close to  , ,
but as  approaches approaches  , the denominator approaches zero, , the denominator approaches zero,
making  increase without bounds. increase without bounds.
However, if a value of  makes both, numerator and denominator zero, makes both, numerator and denominator zero,
there may not be a vertical asymptote at that value.
For example,  does not exist for does not exist for  , but , but  for all for all  , so within its domain , so within its domain  is just a linear function, is just a linear function,
and graphs as a slanted line, with a hole at the point (1,3), and no vertical asymptote.
On the other hand,  is {{g(x)=(x+2)/(x-1)}}} for is {{g(x)=(x+2)/(x-1)}}} for  , ,
and has  for a vertical asymptote. for a vertical asymptote.
A rational function has a horizontal asymptote  for some number for some number 
when numerator and denominator are polynomials of the same degree, and the ratio of the leading coefficients is  . .
It is obvious that  has has  for a vertical asymptote, for a vertical asymptote,
but so does  . .
b. How many different possibilities has an academic coach trying to choose a team of 3 students to represent the school in an academic contest? (The order the team members are chosen or listed does not matter).
EXPLANATION:
Choosing a set of  from a larger set of from a larger set of  , is a question of combinations, because the choosing order, position, or role of each team member is not important. , is a question of combinations, because the choosing order, position, or role of each team member is not important.
When choosing, there are  possibilities for the first choice, possibilities for the first choice,  for the second choice, and for the second choice, and  for the third choice. for the third choice.
That is  . .
But there are  ways to choose the same team, because any of the {{[3}}} members could have been chosen first, followed in each case, by any of the {{[3-1=2}}} other members, leaving just ways to choose the same team, because any of the {{[3}}} members could have been chosen first, followed in each case, by any of the {{[3-1=2}}} other members, leaving just  choice. choice.
So there may be  lists of lists of  members, but since each set of members, but since each set of  can be listed can be listed 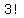 ways, there are really ways, there are really  teams. teams.
NOTE: An alternate word problem is
How many different cheerleading team of  members can be chosen from members can be chosen from  students showing up at the tryouts? students showing up at the tryouts?
c. The equation of an ellipse with vertices at (0,0) and (-8,0) could be
 . .
EXPLANATION:
The points called vertices are the ends of the major axis, since the ends of the minor axis are usually called co-vertices.
The given points are on a horizontal line (axis), so the segments between them has to be the horizontal major axis.
Since the distance between the vertices is  , the semi-major axis is , the semi-major axis is  , and the equation of the ellipse must be , and the equation of the ellipse must be  with any with any  (the semi-minor axis) such that (the semi-minor axis) such that 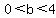 . .
d. 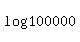 is a logarithmic expression equivalent to 5. So is is a logarithmic expression equivalent to 5. So is  . .
EXPLANATION:
 so so  , and , and
 so so  . .
|
|
|
| |