|
Question 1027806: Please help me and show all steps and work. I am really lost and my professor really is no help. I have been trying to figure this out for days now. I never had any of these types of problems in highschool. Thanks
Find the equation of the parabola that contains the points (-1,10),(2,-5)and(3,-18). Once you found the equation, answer the following questions:
a. Where is the vertex
b. Is the vertex a maximum or minimum
c. Where is the focus
d. Where are the x-intercepts?
Found 2 solutions by Edwin McCravy, addingup:
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The graph of any parabola has the form
y = f(x) = Ax² + Bx + C
(-1,10),(2,-5)and(3,-18).
Since it goes through (-1,10), substitute x=-1 and y=f(x)=10
f(x) = Ax² + Bx + C
10 = A(-1)² + B(-1) + C
10 = 1A - B + C
A - B + C = 10
Since it goes through (2,-5), substitute x=2 and y=f(x)=-5
f(x) = Ax² + Bx + C
-5 = A(2)² + B(2) + C
-5 = 4A + 2B + C
4A + 2B + C = -5
Since it goes through (3,-18), substitute x=3 and y=f(x)=-18
f(x) = Ax² + Bx + C
-18 = A(3)² + B(3) + C
-18 = 9A + 3B + C
9A + 3B + C = -18
So we have this system of 3 equations and 3 unknowns:
 Solve that system either by elimination or substitution
and get A=-2, B=-3, C=9
So the equation
f(x) = Ax² + Bx + C
becomes
f(x) = -2x² - 3x + 9
The vertex is the point
Solve that system either by elimination or substitution
and get A=-2, B=-3, C=9
So the equation
f(x) = Ax² + Bx + C
becomes
f(x) = -2x² - 3x + 9
The vertex is the point 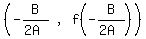


 So the vertex is
So the vertex is 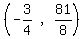 Since the coefficient of A is negative the parabola opens
downward, and the vertex is a MAXIMUM. The focus is BELOW
the vertex.
Since A=-2, the focus is 2 units BELOW the vertex, so we add
A=-2 units to the y-coordinate of the vertex:
Since the coefficient of A is negative the parabola opens
downward, and the vertex is a MAXIMUM. The focus is BELOW
the vertex.
Since A=-2, the focus is 2 units BELOW the vertex, so we add
A=-2 units to the y-coordinate of the vertex:
 For the focus, we use the same x-coordinate as the vertex
So the vertex is
For the focus, we use the same x-coordinate as the vertex
So the vertex is  The x-intercepts are found by setting y = 0:
f(x) = -2x² - 3x + 9
0 = -2x² - 3x + 9
2x² + 3x - 9 = 0
(2x-3)(x+3) = 0
2x-3=0; x+3=0
2x=3; x=-3
x=
The x-intercepts are found by setting y = 0:
f(x) = -2x² - 3x + 9
0 = -2x² - 3x + 9
2x² + 3x - 9 = 0
(2x-3)(x+3) = 0
2x-3=0; x+3=0
2x=3; x=-3
x= So the x-intercepts are the points
So the x-intercepts are the points
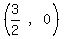 and and 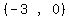 Here is the graph. The points marked are the vertex, focus,
and x-intercepts.
Here is the graph. The points marked are the vertex, focus,
and x-intercepts.
 Edwin
Edwin
Answer by addingup(3677)   (Show Source): (Show Source):
|
|
|
| |