SOLUTION: The measure of a regular polygons interior angle is four time bigger than the measure of its external angle. How many sides does the polygon have?

I + E = 180,     (1)     (the sum of interior I and exterior E angles is 180°)
I = 4E.          (2)     (from the condition).

Substitute (2) into (1). You will get

4E + E = 180   --->   5E = 180   --->   E = 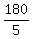 = 36.

So, the exterior angle is 36°. Then the interior angle is 180° - 36° = 144°.


From this point, there are two ways to complete the solution.


First way is to use the fact that the sum of exterior angles of a polygon is 360°.

Then you have an equation

n*36 = 360,

which implies  n = 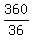 = 10.


Another way is to use the formula for the sum of interior angles of a polygon:

n*144° = (n-2)*180°.

It gives 

n*144 = n*180 - 360,   or
360 = n*180 - n*144,   or
n*36 = 360,

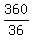and again  n =  = 10.

Answer. The polygon is 10-gon. It has 10 vertices and 10 sides.