Question 1027170: Given odd integers a, b, c, prove that the equation  cannot have a solution x which is a rational number. cannot have a solution x which is a rational number.
Found 2 solutions by richard1234, ikleyn:
Answer by richard1234(7193)   (Show Source): (Show Source):
You can put this solution on YOUR website! Assume otherwise that  has a rational solution has a rational solution  . Then . Then  is rational if and only if the discriminant is rational if and only if the discriminant  is a perfect square (using the quadratic formula, coupled with the fact that a,b,c are integers). is a perfect square (using the quadratic formula, coupled with the fact that a,b,c are integers).
a,b,c are odd. We will show that  cannot possibly be a perfect square by looking at it modulo 8. All of the odd perfect squares (1^2, 3^2, 5^2, 7^2) leave a remainder of 1 when divided by 8. However cannot possibly be a perfect square by looking at it modulo 8. All of the odd perfect squares (1^2, 3^2, 5^2, 7^2) leave a remainder of 1 when divided by 8. However  and and  , so , so  , i.e. b^2 - 4ac always leaves a remainder of 5 when divided by 8. Therefore it cannot be a perfect square, and any real solution x cannot be rational. , i.e. b^2 - 4ac always leaves a remainder of 5 when divided by 8. Therefore it cannot be a perfect square, and any real solution x cannot be rational.
Answer by ikleyn(52835)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Given odd integers a, b, c, prove that the equation  cannot have a solution x which is a rational number. cannot have a solution x which is a rational number.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Assume the equation  = =  with odd integer coefficients a, b an c has the solution,
which is a rational fraction with odd integer coefficients a, b an c has the solution,
which is a rational fraction  with integer p and q.
We can assume that all the common divisors of p and q are just canceled in the fraction with integer p and q.
We can assume that all the common divisors of p and q are just canceled in the fraction  ,
so that p and q are relatively primes integer numbers. In particular, p and q are not both multiples of 2 simultaneously.
Then substitute the fraction ,
so that p and q are relatively primes integer numbers. In particular, p and q are not both multiples of 2 simultaneously.
Then substitute the fraction  into the equation.
You will get into the equation.
You will get 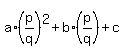 = =  .
Multiply both sides by .
Multiply both sides by  to rid off the denominators. You will get to rid off the denominators. You will get
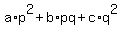 = =  . (1)
Now, if p is odd, then q can not be multiple of 2, otherwise you easily get a contradiction due to equation (1).
Similarly, if q is odd, then p can not be multiple of 2, otherwise you easily get a contradiction due to equation (1).
Thus both p and q must be odd.
Then the equation (1) has three odd addends that sum up to zero, which is impossible.
This contradiction completes the proof. . (1)
Now, if p is odd, then q can not be multiple of 2, otherwise you easily get a contradiction due to equation (1).
Similarly, if q is odd, then p can not be multiple of 2, otherwise you easily get a contradiction due to equation (1).
Thus both p and q must be odd.
Then the equation (1) has three odd addends that sum up to zero, which is impossible.
This contradiction completes the proof.
|
|
|