SOLUTION: Point P is inside rectangle ABCD. Show that PA^2 + PC^2 = PB^2 + PD^2. Be sure that your proof works for ANY point inside the rectangle.

Algebra ->  Geometry-proofs -> SOLUTION: Point P is inside rectangle ABCD. Show that PA^2 + PC^2 = PB^2 + PD^2. Be sure that your proof works for ANY point inside the rectangle.      Log On


   

Question 1027077: Point P is inside rectangle ABCD. Show that
PA^2 + PC^2 = PB^2 + PD^2.
Be sure that your proof works for ANY point inside the rectangle.
Answer by ikleyn(52803) About Me  (Show Source):
You can put this solution on YOUR website!
.
Point P is inside rectangle ABCD. Show that
PA^2 + PC^2 = PB^2 + PD^2.
Be sure that your proof works for ANY point inside the rectangle.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~` 

Let us assume that 

  - the vertice A of the rectangle has the coordinates (0,0)   (lies at the origin)
  - the vertice B                                      (a,0),
  - the vertice C                                      (a,b),   and
  - the vertice D                                      (0,b).

Let the point P is (x,y).

Then 

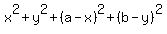PA%5E2+%2B+PC%5E2 = x%5E2+%2B+y%5E2+%2B+%28a-x%29%5E2+%2B+%28b-y%29%5E2.

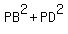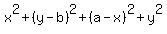PB%5E2+%2B+PD%5E2 = x%5E2+%2B+%28y-b%29%5E2+%2B+%28a-x%29%5E2+%2B+y%5E2,

according to the Pythagorean theorem.

Compare these formulas to make sure that the right sides are equal.

So the left sides are.

Proved.