|
Question 1027061: For the function: (x^3+2x^2-4x-8)/2x^2-8
a) Find the domain of the function, and discuss the behavior of f near any excluded x values.
b) Identify all intercepts
c) Find all vertical, horizontal, and slant asymptotes of the graph of the function.
Found 2 solutions by robertb, KMST:
Answer by robertb(5830)   (Show Source): (Show Source):
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! I assume you meant
 . .
The numerator and denominator of that rational function can be factored.
 . .
When  <---> <---> the denominator is zero, the denominator is zero,
and the function has no defined value.
a) So, the values  are excluded from the domain of the function. are excluded from the domain of the function.
The function can be simplified as
 for for 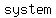 . .
The graph of  is a straight line with two holes, is a straight line with two holes,
and the behavior of  near the excluded values (and everywhere else in its domain) near the excluded values (and everywhere else in its domain)
is just like the behavior of  . .
In other words,  and and  . .
b) The y-intercept of  is is  , ,
or the point (0,1) .
 is never zero, because where the function exists is never zero, because where the function exists
it is equal to  , ,
and  only for only for  which is not part of the domain of which is not part of the domain of  . .
So, there is no x-intercept. The graph of function does not intersect the x-axis; it jumps over it.
c) Since everywhere in its domain  , ,
the line  could be considered the slant asymptote. There is no other asymptote. could be considered the slant asymptote. There is no other asymptote.
|
|
|
| |