SOLUTION: The ratio of the interior angles of a pentagon is 4:4:5:5:6, find the largest interior and exterior angles.

Let A, B, C, D and E be the interior angles of the given pentagon, in the corresponding ordering.
The condition means that there is an angle which is the common measure of the given angles.
Let x be the measure of this angle.

Then A = 4x, B = 4x, C = 5x, D = 5x, E = 6x.

The sum of interior angles of the pentagon is (5-2)*180° = 3*180° = 540°.

It gives an equation

4x + 4x + 5x + 5x + 6x = 540°,   or

24x = 540°.

Then x = 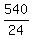 = 22.5°.

Therefore, the interior angles are 

A = 4*22.5° = 90°,  B = 90°,  C = 112.5°,  D = 112.5°,  E = 135°.

The largest interior angle is C = 135°.
The largest exterior is 90°.