SOLUTION: The sides of the bases of a frustum of a regular pyramid are 6 cm and 5 cm, the lateral face makes a 60 degree angle with the horizontal. Compute the volume of the frustum of the p

I will give you the idea only, and will not go in details.

1. Make a sketch. Draw the entire pyramid and the plane which cut off the frustum. 
   Also draw the slant height and mark that part of the slant height which belongs to the lateral face of the frustum.

2. Using the fact that the (lower) base is the regular hexagon, compute the apothem of this hexagon. It is 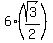 =  cm.

3. Next, since the lateral face makes a 60 degree angle with the horizontal, the height of the 
   entire pyramid is 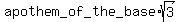 =  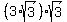= 9 cm.

4. Since the ratio of the upper and lower base edges is 5:6, it means that the whole slant height is 6 times 
   its part belonging to the frustum lateral face. In other words, the whole slant height of the pyramid 
   is 6 times longer than the part of this slant height belonging to the frustum lateral side.

5. It implies that the height of the pyramid is 6 times the height of the frustum. Hence, the height of the frustum is  = 1.5 cm.

6. Now you have everything to calculate the volume of the frustum.
   Calculate first the volume of the entire pyramid. You just know its height: it is 9 cm.
   Then calculate the volume of the upper (smaller) pyramid. Its height is 9 cm - 1.5 cm = 7.5 cm.
   Then distract smaller volume from the greater volume.

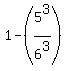   Or simply, after calculating the volume of the larger pyramid, take  of its volume as the volume of the frustum.

7. That's it.