.
A small pipe can fill a vat with water in 8 hours. A larger pipe can fill the same vat in only 6.5 hours.
How long would it take to fill the vat if the two pipes are working at the same time?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
A small pipe's rate is  vat-volume-per-hour.
A large pipe's rate is
vat-volume-per-hour.
A large pipe's rate is 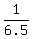 vat-volume-per-hour.
When both pipes work, their combined rate is
vat-volume-per-hour.
When both pipes work, their combined rate is
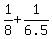 =
= 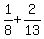 =
=  =
= 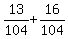 =
= 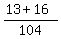 =
= 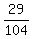 .
It means that two pipes working together fill
.
It means that two pipes working together fill 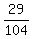 of the vat volume per hour.
Hence, they will fill the vat in
of the vat volume per hour.
Hence, they will fill the vat in 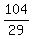 hours.
Unfortunately, these numbers and this ratio are so curve, that the question arises:
who invented this condition and for what purposes. Definitely, it was not me.
If you want to see more solved problems on joint work, look into the lesson
Using fractions to solve word problems on joint work in this site.
They are really nice problems, and you really will benefit from reading it.
hours.
Unfortunately, these numbers and this ratio are so curve, that the question arises:
who invented this condition and for what purposes. Definitely, it was not me.
If you want to see more solved problems on joint work, look into the lesson
Using fractions to solve word problems on joint work in this site.
They are really nice problems, and you really will benefit from reading it.