Question 1026243: Hello, could someone please clarify the Triangle Inequality Theorem? I am trying to determine if it is possible to construct a triangle with sides 4, 5, and 9. If I take the long side, 9 and then add 4+5, it is not more than 9....therefore, not possible to make a triangle with these sides. But, if I take 5+9, they do equal more than the 3rd side. I thought the sum of the lengths of ANY two sides of a triangle is greater than the length of the 3rd side. Am I interpreting this the wrong way??? Help, confused! Thanks!
Found 2 solutions by josgarithmetic, MathTherapy:
Answer by josgarithmetic(39627)   (Show Source):
You can put this solution on YOUR website! Gaining a solid intuitive understanding about this theorem will enable you to think through the question and answer it.
Try taking any two lengths, known lengths if you wish; and you know you need ONE MORE length if you want to form a triangle. Try as example, lengths 7 and 10. Can the next length to choose be 7+10=17 and allow formation of a triangle?
.....NO!
Why?
Try choosing a smaller length instead.
Can you choose length of 16 and form a triangle?
Should be YES.
Now, instead of choosing 17 or 16, try choosing 18.
Can you form a triangle using lengths 7, 10, and 18?
...
.... NO!
Why?
-----
Now, can you go back to your given three sides of 4, 5, and 9, and determine if these can form a triangle?
Answer by MathTherapy(10556)  (Show Source):
You can put this solution on YOUR website!
Hello, could someone please clarify the Triangle Inequality Theorem? I am trying to determine if it is possible to construct a triangle with sides 4, 5, and 9. If I take the long side, 9 and then add 4+5, it is not more than 9....therefore, not possible to make a triangle with these sides. But, if I take 5+9, they do equal more than the 3rd side. I thought the sum of the lengths of ANY two sides of a triangle is greater than the length of the 3rd side. Am I interpreting this the wrong way??? Help, confused! Thanks!
The Triangle Inequality Theorem states that the 3rd side of a triangle is GREATER than the difference between the other 2 sides,
but LESS THAN their sum.
Taking the 2 sides: 4 and 5, and by letting the 3rd side = T, we get: 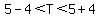 =  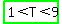. This indicates that the 3rd side,
T (in this case, 9) MUST be > 1 but < 9. However, the 3rd side is 9, so such a triangle is IMPOSSIBLE to construct
|
|
|
