Question 10258: My math problem is this:
A car goes from point A to point B, at a rate of 40 mph. Then the same car turns around and goes from point B to point A, at a rate of 60 mph. What is the average speen of this car? My teacher said that it was not 50 mph. I am very confused on this and would like a thurough explination. Thank you so much for this. :D I need all the help, and it is very much appreciated. I've spent time trying to figure out the answer to this, and I've come up with an average speed of 55 mph, but I am not sure how I got that, and I don't know how to check if it is right. Please help me and thank you.
Answer by rapaljer(4671)   (Show Source): (Show Source):
You can put this solution on YOUR website! Please note: the previously posted solution to this problem is WRONG!
Let there be NO MISTAKE!

What is NOT given in this problem, which turns out actually to be irrelevant, is the total distance between A and B.
Since it really doesn't matter, you can pick any value for the distance, any arbitrary number to make the math easier to do. Notice that the rates of the car going is 40 mph, and returning the rate is 60 mph. It makes an easier math problem if you choose a distance that is a multiple of 40 and 60, say 120 miles. If you picked a different distance, the result will be exactly the same. As Mentioned above, you must find the total distance driven and the total time it took to travel. Obviously, if it is 120 miles going and 120 miles coming, then the total distance traveled is 240 miles.
Since  , ,  . .
Time going =  = 3 hours. = 3 hours.
Time returning=  = 2 hours. = 2 hours.
Total time for the trip both ways = 2+3 = 5 hours.
 = =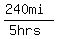 = 58 mph. = 58 mph.
R^2 at SCC
|
|
|