Question 1025763: A petroleum company has two different sources of crude oil. The first source provides crude oil that is 65% hydrocarbons, and the second one provides crude oil that is 90% hydrocarbons. In order to obtain 170 gallons of crude oil that is 75% hydrocarbons, how many gallons of crude oil must be used from each of the two sources?
Answer by ikleyn(52788)   (Show Source):
You can put this solution on YOUR website! .
A petroleum company has two different sources of crude oil. The first source provides crude oil that is 65% hydrocarbons, and the second one provides crude oil that is 90% hydrocarbons. In order to obtain 170 gallons of crude oil that is 75% hydrocarbons, how many gallons of crude oil must be used from each of the two sources?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let x = volume of the crude oil that is 65% hydrocarbons (in gallons),
and y = volume of the crude oil that is 90% hydrocarbons.
Then you have two equations:
x + y = 170, (1) (for the total volume)
0.65x + 0.9y = 0.75*170. (2) (for the hydrocarbon content).
Rewrite simplifying (2):
x + y = 170, (1')
0.65x + 0.9y = 127.5. (2')
From (1'), express x = 170-y and substitute it into (2'). You will get a single equation for y:
0.65*(170-y) + 0.9y = 127.5
Simplify and solve it:
110.5 - 0.65y + 0.9y = 127.5,
0.25y = 127.5 - 110.5,
0.25y = 17,
y = 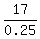 = 68 gallons. It is the volume of the crude oil that is 90% hydrocarbons.
Now, the volume the crude oil that is 65% hydrocarbons is 170 - 68 = 102 gallons.
|
|
|
