Question 1024805: KSDLD-Pros, an IT Project consulting firm, is forming an IT Project management team of 5 professionals. In the firm of 50 professionals, 8 are considered to be data analytics specialists. If the professionals are selected at random, what is the probability that the team will include...
a. no data analytics specialist?
b. at least one data analytics specialist?
Answer by mathmate(429)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Question:
KSDLD-Pros, an IT Project consulting firm, is forming an IT Project management team of 5 professionals. In the firm of 50 professionals, 8 are considered to be data analytics specialists. If the professionals are selected at random, what is the probability that the team will include...
a. no data analytics specialist?
b. at least one data analytics specialist?
Solution:
The hypergeometric distribution will be used.
A=number of Analytics specialists in the population (8)
B=number of non-Analytics specialists in the population (42)
a=number of Analytics specialists chosen in the sample (x)
b=number of non-Analytics specialists chosen in the sample (5-x)
and
C(n,r)=n!/(r!(n-r)!) is the binomial coefficient of taking r out of n objects
then
P(a,a+b) [choosing a specialists out of (a+b)]
=C(a,A)*C(b,B)/C(a+b,A+B) [hypergeometric distribution]
(a) No analytics specialist (x=0, a=0, b=5)
P(a,a+b)
P(0,5)
=C(8,0)*C(42,5)/C(50,5)
=1*850668/2118760
=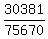
=0.4015 (approx.)
(b)At least one analytics specialist
Since this case is the complement of case (a), the result is
P(1≤x≤5;5)
=1-P(0,5)
=0.5985 (approx.)
On the other hand, if we would have used (incorrectly) the binomial distribution, then p=0.2, n=0,
(a) P(0,5)=C(0,5)*0.2^0*(0.8^5)=0.328
This problem has a relatively small population (50)from which a relatively large sample (5) is taken. Use of the binomial distribution will only provide an approximation, since the probability of choosing a analytics specialist (varies from 20% to a minimum of 11%) varies during the experiment.
So it is important to choose the right distribution for a given application.
|
|
|