Question 102451: The demand and supply equations for a certain item are given by
D = –5p + 40 S = –p2 + 30p – 8
Find the equilibrium price.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Can you double check my work for me? I think it is right.
A rectangular garden is to be surrounded by a walkway of constant width.
The garden's dimensions are 30 ft by 40 ft. The total area, garden plus walkway, is to be 1800 ft2. What must be the width of the walkway to nearest thousandth?
Answer: x=3.860
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Is the following trinomial a perfect square? x2 – 18x + 81
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Identify the axis of symmetry, create a suitable table of values, then sketch the graph (including the axis of symmetry). y = –x2 + 1
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Answer by edjones(8007)   (Show Source): (Show Source):
You can put this solution on YOUR website! A.
-5p+40=-p^2+30p-8
p^2-35p+48=0
| Solved by pluggable solver: SOLVE quadratic equation (work shown, graph etc) |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=1033 is greater than zero. That means that there are two solutions:  . .


Quadratic expression 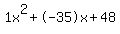 can be factored: can be factored:

Again, the answer is: 33.5701586799882, 1.4298413200118.
Here's your graph:
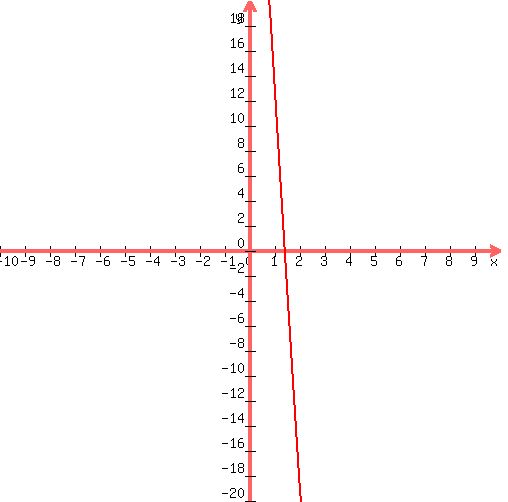 |
B.
(30+x)(40+x)=1800
1200+70x+x^2=1800
x^2+70x-600=0
| Solved by pluggable solver: SOLVE quadratic equation (work shown, graph etc) |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=7300 is greater than zero. That means that there are two solutions:  . .


Quadratic expression 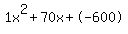 can be factored: can be factored:

Again, the answer is: 7.72001872658765, -77.7200187265877.
Here's your graph:
 |
C.
Yes.
D.
y = –x2 + 1
axis of symetry=0
Ed
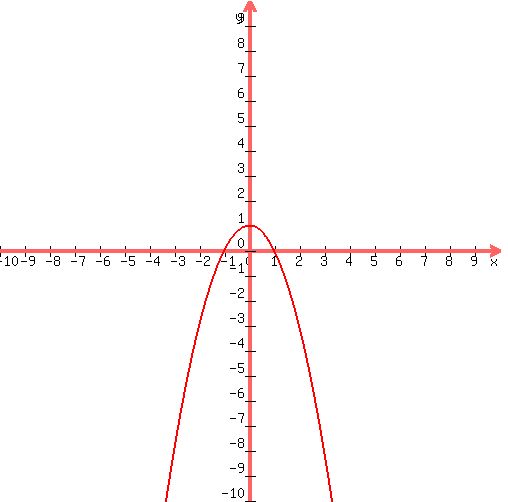
|
|
|