Question 1024431: v the units' digit is twice the tens' digit. Find the numeral.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! WITH TWO VARIABLES:
 = tens' digit (so = tens' digit (so  and and  is an integer) is an integer)
 = units' digit (so = units' digit (so  and and  is an integer) is an integer)
The problem says that "the units' digit is twice the tens' digit,"
so  , which means , which means 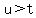 , since , since  . .
The problem also says that "the difference between the digits in a two-digit numeral is 3."
That means that
 . .
So we could say that we are going to solve the system og linear equations
 by substitution, by substitution,
meaning that we will substitute the expression  for for  in in  . .
We get  --> --> , ,
and substituting  for for  in in  , we get , we get
 --> --> . .
So,  , and the number is , and the number is  . .
WITH ONE VARIABLE:
 = the tens' digit. = the tens' digit.
So the units digit, which is "twice the tens' digit", is  , ,
and the difference between the digits is 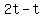 , ,
which according to the problem is  . .
Our equation is  , which simplifies to , which simplifies to  . .
So  is the tens' digit; is the tens' digit;
 is the units digit, is the units digit,
and the number is  . .
GUESS AND CHECK METHOD:
The tens' digit cannot be  , because then the number would not really be "a two-digit numeral". , because then the number would not really be "a two-digit numeral".
The tens' digit cannot be  , because then "the units" digit" would have to be , because then "the units" digit" would have to be  , which is not a digit. , which is not a digit.
For the same reason, the tens' digit cannot be more than  . .
So, the tens' digit must be  , , 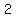 . .
If the tens' digit were  , the units' digit would be , the units' digit would be  , ,
and the two-digit numeral would be  , ,
but the difference between the digits would be  , ,
so  is not the two-digit numeral. is not the two-digit numeral.
If the tens' digit were  , the units' digit would be , the units' digit would be  , ,
and the two-digit numeral would be  , ,
but the difference between the digits would be  , ,
so  is not the two-digit numeral. is not the two-digit numeral.
If the tens' digit were  , the units' digit would be , the units' digit would be  ; ;
the two-digit numeral would be  , ,
and the difference between the digits would be  , as the problem says , as the problem says
so  is the two-digit numeral. is the two-digit numeral.
|
|
|