|
Question 1023909: THIS IS AN ALGEBRAIC FUNCTIONS VARIATIONS PROBLEM. There is also a constant k that is part of the equation I have to create. Can someone go through the logic for this problem?
Kepler's Third Law states that the square of time T required for a planet to complete one orbit around the sun (the period, that is, the length of one planetary year) is directly proportional to the cube of average distance d of the planet from the sun. For the planet Earth, assume d = 93 x 10^6 miles an T = 365 days. Find a) the period of Mars, given that Mars is approximately 1.5 times as distant from the sun as Earth; b) the average distance of Venus from the sun, given that the period of Venus is approximately 223 Earth days.
The units for Part a are in days and the units for part b are in miles.
Found 2 solutions by josgarithmetic, KMST:
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
You can put this solution on YOUR website! ...the square of time T required for a planet to complete one orbit around the sun (the period, that is, the length of one planetary year) is directly proportional to the cube of average distance d of the planet from the sun.
The phrase, "is directly proportional to..." becomes  . .

For the rest, solve for k and use the data to evaluate k and answer the last question.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Stated in formulas, rather than words,
Kepler's Third Law states that
if  = time required for a planet to complete one orbit around the sun (the period, that is, the length of one planetary year), and = time required for a planet to complete one orbit around the sun (the period, that is, the length of one planetary year), and
 = average distance of the planet from the sun, = average distance of the planet from the sun,
then  , ,
where  is the proportionality constant. is the proportionality constant.
So, for Earth, 
For the planet Earth, assume 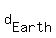 = = 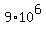  an an   . .
Since we are going to measure times in Earth days and distances in miles
(or in whatever units we want, but using the same units all along),
we do not need to keep writing the units with the calculations.
NOTE: I did not solve for  and I did not use the given average distance between Earth and the sun, because it would only complicate the calculations. and I did not use the given average distance between Earth and the sun, because it would only complicate the calculations.
If your teacher insist that you do it, I am sorry for both of you.
a) They tell us that 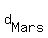 = = 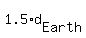 , ,
and according to Kepler's Third Law
 , so , so








 (rounded). (rounded).
So, the period of Mars is approximately 671 days.
b) They tell us that  , ,
and according to Kepler's Third Law
 , and , and  , ,
so with distances in miles this time
 , and , and  . .
Dividing one equation by the other,








 (rounded). (rounded).
So, the the average distance of Venus from the sun, is approximately 67 x 10^6 miles.
|
|
|
| |