Question 1023481: Two trains start heading toward each other from two cities, the distance between which is 720 km, and meet right in the middle. The second train left 1 hour after the first train, but traveled at a speed 4 km/hour faster than the first train. Find the speed of both trains.
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! Two trains start heading toward each other from two cities, the distance between which is 720 km, and meet right in the middle.
The second train left 1 hour after the first train, but traveled at a speed 4 km/hour faster than the first train.
Find the speed of both trains.
:
If they met half-way, each train traveled 360 mi
let s = speed of the slower train
then
(s+4) = speed of the faster train
:
Write a time equation
Slow train time - fast train time = 1 hr
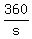 - - 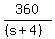 = 1 = 1
multiply equation by s(s+4), cancel the denominators
360(s+4) - 360s = s(s+4)
360s + 1440 - 360s = s^2 + 4s
A quadratic equation
0 = s^2 + 4s - 1440
Use the quadratic formula; a=1; b=4; c=-1440. but this will factor to:
(s-36)(s+40) = 0
positive solution
s = 36 mph, speed of the slow train
then obviously;
40 mph, the speed of the faster
:
:
Check this by finding the actual time of each
360/36 = 10 hrs
360/40 = 9 hrs, 1 hr less
|
|
|