Question 1023433: Graph the function f(x) = x+sqrt(abs(x)).
Consider the behavior of the function at the point (-1,0) and at the origin. Find the limit as x approaches -1 and as x approaches 0.
What is different about the behavior of f(x) near those points? Explain.
Next, graph its derivative. Discuss differentiability at -1 and 0.
Answer by robertb(5830)   (Show Source):
You can put this solution on YOUR website! The roots of the function are at x = -1 and x = 0.
As x approaches -1 from both sides, y approaches 0. For negative x,
 .
To find the limit at x = 0, the left-hand limit (through negative values) is  , while the right-hand limit (through positive values) is  .
Thus 
For x < 0, f'(x) = 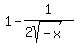 , hence the derivative exists for all such x values, and the graph of f(x) is smooth there. Incidentally, at x = -1, f'(-1) = 1/2.
For x >0, f'(x) =  , hence the the derivative exists for all such x values, and the graph of f(x) is smooth there.
For x = 0:
The left hand derivative at x = 0 is 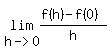 through negative values of h..
= 
= 
= 
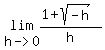
The right hand derivative at x = 0 is 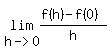through positive values of h..
= 
= 
= 
hence the left-hand and right-hand derivatives are not equal (and opposite infinites) and so there is a cusp at x = 0.
The graph of f(x) is as follows:
 , and
its derivative f'(x):
|
|
|
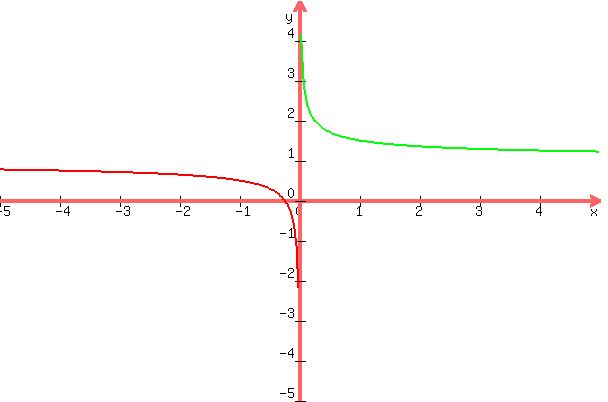
