Question 1023098: Cannot determine the common ratio for:
Sequence: 4,-9, 16, -25,...
Series: 1 - 1/4 + 1/9 - 1/25 + ...
Must create a general term for both, and prove the convergence of the second using the alternating series test.
Answer by ikleyn(52787)   (Show Source):
You can put this solution on YOUR website! .
Cannot determine the common ratio for:
Sequence: 4,-9, 16, -25,...
Series: 1 - 1/4 + 1/9 - 1/25 + ...
Must create a general term for both, and prove the convergence of the second using the alternating series test.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~``
1. I can not also.
They are not Geometric progression. Neither first, nor the second.
2. The general term for the first sequence is 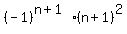 , n = 1, 2, 3 . . .
3. The alternating series test says: if  decreases monotonically and  =  when n -->  ,
then the alternating series converges.
For your series the condition is valid, so the conclusion is valid too.
|
|
|
