Question 1022912: What is the scale factor of each if the polygons are proportional? Please show how you got your answer so I can follow the steps to be able to do it on my own. Thank you for your time and help.
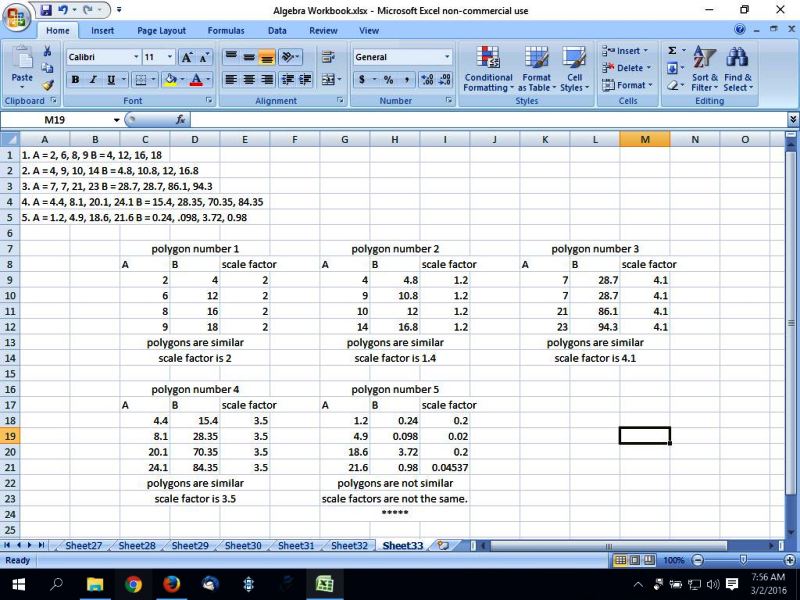
1. A = 2, 6, 8, 9 B = 4, 12, 16, 18
2. A = 4, 9, 10, 14 B = 4.8, 10.8, 12, 16.8
3. A = 7, 7, 21, 23 B = 28.7, 28.7, 86.1, 94.3
4. A = 4.4, 8.1, 20.1, 24.1 B = 15.4, 28.35, 70.35, 84.35
5. A = 1.2, 4.9, 18.6, 21.6 B = 0.24, .098, 3.72, 0.98
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1. A = 2, 6, 8, 9 B = 4, 12, 16, 18
2. A = 4, 9, 10, 14 B = 4.8, 10.8, 12, 16.8
3. A = 7, 7, 21, 23 B = 28.7, 28.7, 86.1, 94.3
4. A = 4.4, 8.1, 20.1, 24.1 B = 15.4, 28.35, 70.35, 84.35
5. A = 1.2, 4.9, 18.6, 21.6 B = 0.24, .098, 3.72, 0.98
if the polygons are similar, then corresponding sides are proportional.
this means that the scale factor is the same for all sides.
if the scale factor is not the same, then the polygons are not similar.
let's look at each in turn.
all you have to do is find the scale factor of one of the corresponding sides and then look at the others to make sure that they all have the same scale factor.
if they do, then the polygons are similar.
if they don't, then the polygons are not similar.
here's my analysis.
|
|
|