SOLUTION: Solve the linear system by graphing. X+2y=1 -2x+y=-4 When I solved this problem I got (2,-1/2), but I don't think I did the problem correctly. Thank you!

You must be very accurate when you solve a system of equations
by graphing. You must use graph paper with large squares and 
use a ruler.

Make a table of points for each line:

 x | y      x | y
 1 | 0      1 |-2 
 3 |-1      3 | 2
-1 | 1     -1 |-6


Plot those points and draw lines through them, using
graph paper and a ruler:



So you see the lines cross at a point that has fractions for both
coordinates.  It's a good idea to draw a vertical and a horizontal
line (in red below) to the x and y-axis, like this:


 

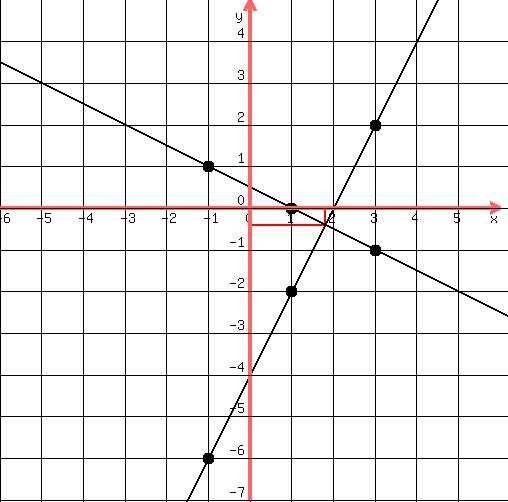It looks like the x coordinate is a little less than 2,
but not close enough to be 1.9, so I'd guess x = 1.8.
The y coordinate is a little less than halfway to -1,
which would be -0.5, but closer to -0.5 than the other 
was to 2, so I'd guess that it is y = -0.4

That's the best you can do with graphing.

Edwin