SOLUTION: solve for x in 4^5x×2^(3x)2=256

It's impossible to tell from that what's part of exponent 
and what is not. When typing everything all on one line, 
you must use parentheses to enclose each part, remembering 
that the rule is PEMDAS so it won't be ambiguous.  It could 
be interpreted as any of these or some others, all which 
have different solutions:

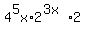
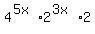
 or  or 

I will arbitrarily assume it's



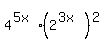
Write 4 as 22 and 256 as 28



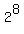When the base of an exponential is itself an exponential,
we simplify by multiplying exponents across the parentheses:



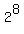Now we add the exponents of 2 on the left in order to
multiply exponentials with the same base 2:



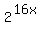
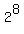Since we have a single power of 2 on both sides, we
can drop the base 2 and equate the exponent:







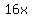
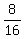
Edwin