|
Question 1021597: Hello, this was in one of my sequence/series questions.
Im pretty sure its got something to do with geometric series, but i dont know how to problem solve using the formula.
Please help!
A bouncy ball is dropped from a height of h meters and allowed to bounce indefinitely. Each succeeding bounce is 0.8 of the preceding one...
If the total vertical distance traveled by the ball is 63 meters, from what height was the ball dropped?
Thank you very much
Found 3 solutions by stanbon, rothauserc, FrankM:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! A bouncy ball is dropped from a height of h meters and allowed to bounce indefinitely. Each succeeding bounce is 0.8 of the preceding one...
If the total vertical distance traveled by the ball is 63 meters, from what height was the ball dropped?
Thank you very much
------
You are correct; it's an infinite geometric series.
-----------------
h, 0.8h, 0.8^2h, ...
-----------------------------
S(n) = a/(1-r)
---
Your Problem::
S(n) = h/(1-0.8) = h/0.2 = 10h/2 = 5h
-----------
Solve:: 5h = 63 meters
height = 12.6 meters
Cheers,
Stan H.
-----------
Answer by rothauserc(4718)   (Show Source): (Show Source):
You can put this solution on YOUR website! You need to sum the geometric series
:
the sum begins at h
:
note that the ball has to bounce up and down, then
:
we need the summation from 0 to infinity of 2h(0.8)^n
:
we are give total vertical distance is 63 meters
:
if we ignore the multiplier, a geometric series will sum o to infinity to
:
1(1 - r) = 1 / (1 - 0.8) = 10 / 2 = 5
:
63 = 5(2h) - h
note we have to subtract h since we counted it and it does not count :-)
63 = 9h
9h = 63
**********************
h = 7 meters
the ball was dropped from 7 meters
*********************
Answer by FrankM(1040)   (Show Source): (Show Source):
You can put this solution on YOUR website! The infinite series summation is 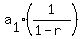 where where  is the first term of the series, and r is the geometric multiplier. is the first term of the series, and r is the geometric multiplier.
Say you were given 1+1/2+1/4+1/8+..... can you see that this adds to 2? Take 2 squares, the first is "1" of course then take the second and cut it in half with a line, then the remaining half to quarters. It reproduces the series, and from the equation -

Now, your problem is tricky as there are 2 series to add, H(1+.8+.64+.512.....) this is vertical distance dropped. But you need to add the distance it goes up, H(.8+.64+.512.....) see how the first "up" is .8 the height of the drop?
Let's solve the first series -
1+.8+.64+.512... (we'll multiply by H after solving this)
 and r=.8 and r=.8

So the first series adds to 5H
The second series
.8+.64+.512..
 and r=.8 and r=.8

So this adds to 4H which makes sense, as the "up" is .8 times the prior "down".
Now, you've calculated that from a drop of H and a boucyness of .8, you get a total travel of 9H.
One final step. They told you the travel was 63 meters.
9H = 63m
H=63/9 m
H= 7m
Now you can solve an infinite number of infinite geometric series equations.....
NOTE: The tutors here have no way to communicate with each other. I believe the other 2 answers are wrong. Stanbon did not include the "up" distance. The problem states "total vertical distance traveled" .
Roth started at .8h which ignored the initial drop, the first full 1h. (Edit again - Roth has corrected and confirmed my answer)
|
|
|
| |