Question 1021088: In a certain country, the true probability of a baby being a boy is 0.516. Among the next five randomly selected births in the country, what is the probability that at least one of them is a girl?
Answer by mathmate(429)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Question:
In a certain country, the true probability of a baby being a boy is 0.516. Among the next five randomly selected births in the country, what is the probability that at least one of them is a girl?
Solution:
The given problem satisfies the criteria for modelling with the binomial distribution:
- probability (p=0.516) remains constant throughout the experiment of a known number (n=5) of trials.
- the experiment is a series of Bernoulli trials (B=event of a boy, ~B=event of a girl).
- all trials are independent and random.
The equation to calculate X successes (B) out of n trials with probability of success (p) is given by:
P(X;n;p)=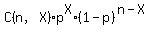
and C(n,X) is the combination of X items out of n = n!/(X!(n-X)!).
Here
n=5, p=0.516, X={1,2,3,4,5}
P(X={1,2,3,4,5};n;p)
=1-P(X=0;n;p) [= 1 - complement of the required probability]
=1-C(5,0)*0.516^0*(1-0.516)^5
=1-1*1*0.484^5
=0.9734
|
|
|